动态规划 | DP ¶
约 1952 个字 2 张图片 预计阅读时间 8 分钟
动态规划是一种求解多阶段决策过程最优解的方法,包括以下内容:
- 基本概念:包括阶段、状态、决策、策略等。
- 最优化原理和最优化定理:最优策略的子策略是对应子问题的最优策略。
- 状态无后效性:某阶段的状态确定后,此后过程的演变不再受此前各状态及决策的影响。
- 动态规划的逆序解法和顺序解法:两种不同的求解顺序,但本质相同。
基本概念与建模 ¶
- 阶段:问题过程按时间、空间的特征分解成若干相互联系的阶段。
- 状态:k 阶段开始(或结束)时的客观条件,记为 \(s_k \in S_k\),\(S_k\) 为 \(k\) 阶段状态集合
- 决策:依据状态做出的决定,记为 \(u_k(s_k)\in D_k(s_k)\) , \(Dk (sk)\) 为状态 \(s_k\) 的允许决策集合。
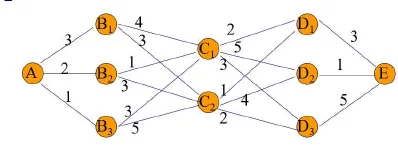
如 \(D_1(A) = {B_1,B_2,B_3},u_1(A) = B_i \quad i = 1,2,3\) 4. 状态转移方程:描述当前状态在给定决策下转移至下一阶段的过程;\(s_{k+1}=T_k(s_k, u_k (s_k))\) 5. 指标函数: 评价沿子策略 \(P_{k,n}\) 过程性能优劣的函数,记为 \(V_{k,n}(s_{k}, p_{k,n})\)。
基本原理与求解 ¶
顺序逆序 ¶
顺序解法和逆序解法无本质区别 若初始状态给定时,用逆序解法比较简单。 反之,用顺序解法简单。
状态的无后效性¶
已经求解的子问题,不会再受到后续决策的影响。
后部子过程策略,从 k 阶段开始到终了阶段的决策子序列,记为 \(p_{s,n}(s_k) = \{u_k \left(s_k\right), u_{k+1}\left(s_{k+1}\right),\dots, u_n\left(s_n\right)\} \in P_{k,n} (s_k)\)
最优化原理:最优策略的子策略是对应子问题的最优策略。
最优化定理 ¶
策略 \(p^*_{l,n}\) 是最优策略的充要条件是,对于所有的 k,都有: $$ begin{array}{l} V_{1,n}left({s_{l}}, p_{1, n}^{*}right) \ quad=mathop{opt}limits_{p_{l, k-1} in p_{l, k-1}} V_{1, k-1}left(s_{1}, p_{1, k-1}right)+mathop{opt}limits_{p_{k, n} in p_{k, n}} V_{k, n}left(s_{k}, p_{k, n}right) end{array} $$
新的最短路节点必定从已知的最短路节点展开
贝尔曼最优性
贝尔曼最优性原理的数学表达通常涉及两个方程:贝尔曼期望方程和贝尔曼最优方程。
贝尔曼期望方程(Bellman Expectation Equation)¶
对于一个给定的策略 \(\pi\),贝尔曼期望方程描述了值函数 \(V^{\pi}(s)\) 和 \(Q^{\pi}(s,a)\) 之间的关系:
其中,\(s\) 是当前状态,\(a\) 是动作,\(r(s,a)\) 是状态 - 动作对的奖励,\(\gamma\) 是折扣因子,\(P(s'|s,a)\) 是状态转移概率。
对于 \(Q\) 值函数,贝尔曼期望方程可以表示为:
贝尔曼最优方程(Bellman Optimality Equation)¶
贝尔曼最优方程描述了最优值函数 \(V^{*}(s)\) 和 \(Q^{*}(s,a)\) 之间的关系:
其中,\(\max_{a}\) 表示对于所有可能的动作 \(a\) 取最大值。
对于 \(Q\) 值函数,贝尔曼最优方程可以表示为:
贝尔曼最优方程表明,最优值函数可以通过将奖励和折扣后的期望值函数最大化来计算。它还暗示了最优策略可以通过选择导致最大 \(Q\) 值的动作来确定。
应用举例 ¶
算法之动态规划总结(11 种 DP 类型,70 道全部搞懂)_dp 算法 -CSDN 博客
1、线性 DP ¶
最经典单串:
- 300: 最长上升子序列 (medium)
其他单串
- 32: 最长有效括号 (hard)
- 376: 摆动序列 (medium)
- 368: 最大整除子集 (medium)
- 410: 分割数组的最大值 (hard)
最经典双串: 1143: 最长公共子序列 (medium)
其他双串 97: 交错字符串 (medium) 115: 不同的子序列 (hard) 583: 两个字符串的删除操作 (medium)
经典问题: 53: 最大子序和 (easy) 120: 三角形最小路径和 (medium) 152: 乘积最大子数组 (medium) 354: 俄罗斯套娃信封问题 (hard) 887: 鸡蛋掉落(DP+ 二分)(hard)
打家劫舍系列:( 打家劫舍 3 是树形 DP) 198: 打家劫舍 (medium) 213.打家劫舍 II 中等
股票系列: 121.买卖股票的最佳时机 122: 买卖股票的最佳时机 II (medium) 123: 买卖股票的最佳时机 III (hard) 188: 买卖股票的最佳时机 IV (hard) 309: 最佳买卖股票时机含冷冻期 (medium) 714: 买卖股票的最佳时机含手续费 (medium)
字符串匹配系列 72: 编辑距离 (hard) 44: 通配符匹配 (hard) 10: 正则表达式匹配 (hard)
其他 375: 猜数字大小 II (medium)
2、区间 DP ¶
5: 最长回文子串 (medium) 516.最长回文子序列
87: 扰乱字符串 (hard) 312: 戳气球 (hard) 730: 统计不同回文子字符串 (medium) 1039: 多边形三角剖分的最低得分 (hard) 664: 奇怪的打印机 (medium) 1246: 删除回文子数组 (medium)
3、背包 DP ¶
377: 组合总和 Ⅳ (medium) 416: 分割等和子集 (01 背包 - 要求恰好取到背包容量) 494: 目标和 (01 背包 - 求方案数) 322: 零钱兑换 (完全背包) 518: 零钱兑换 II (完全背包 - 求方案数) 474: 一和零 (二维费用背包)
4、树形 DP ¶
124: 二叉树中的最大路径和 (hard) 1245: 树的直径 (邻接表上的树形 DP) (medium) 543: 二叉树的直径 (easy) 333: 最大 BST 子树 (medium) 337: 打家劫舍 III (medium)
5、状态压缩 DP ¶
464: 我能赢吗 (medium) 526: 优美的排列 (medium) 935: 骑士拨号器 (medium) 1349: 参加考试的最大学生数 (medium)
6、数位 DP ¶
233. 数字 1 的个数 困难 902.最大为 N 的数字组合 1015.可被 K 整除的最小整数
7、计数型 DP ¶
计数型 DP 都可以以组合数学的方法写出组合数,然后 dp 求组合数 62: 不同路径 (medium) 63: 不同路径 II (medium) 96: 不同的二叉搜索树 (medium) 1259: 不相交的握手 (卢卡斯定理求大组合数模质数)
8、递推型 DP ¶
70. 爬楼梯 509.斐波那契数
576: 出界的路径数 (medium) 688: “马”在棋盘上的概率 (medium) 935: 骑士拨号器 (medium) 957: N 天后的牢房 (medium) 1137: 第 N 个泰波那契数 (medium)
9、概率型 DP ¶
求概率,求数学期望 808: 分汤 (medium) 837: 新 21 点 (medium)
10、博弈型 DP ¶
策梅洛定理,SG 定理,minimax
翻转游戏 293: 翻转游戏 (medium) 294: 翻转游戏 II (medium)
Nim 游戏 292: Nim 游戏 (medium)
石子游戏 877: 石子游戏 (medium) 1140: 石子游戏 II (medium)
井字游戏 348: 判定井字棋胜负 (medium) 794: 有效的井字游戏 (medium) 1275: 找出井字棋的获胜者 (medium)
11、记忆化搜索 ¶
本质是 dfs + 记忆化,用在状态的转移方向不确定的情况 329: 矩阵中的最长递增路径 (medium) 576: 出界的路径数 (medium)
旅行商(货郎担)问题 ¶
设备更新问题 ¶
可靠性问题 ¶
控制问题 ¶
离散系统的最优控制
最优控制理论 九、Bellman 动态规划法用于最优控制 _cost-to-go-CSDN 博客